Angelo A. Mazzotti
Maths is a game and
in every game there is Mathss
Angelo is
MA in Mathematics
PhD in Operations Research
High School teacher (in Italian and German)
Game inventor
Highlights
NEW GAME soon out on BOARD GAME ARENA (designed by Sophie Püschmann)
3 & 4: THE GAME
NEW GAME (designed by Sophie Püschmann)
DIE SPIELEFABRIK
MOST RECENT PAPER
Die versteckte Schönheit im Korbschen Oval der Bibliothek zu Wolfenbüttel (with A. Ilchmann - link to preprint).
PAPERS RECENTLY ACCEPTED FOR PUBLICATION
A method for recognising oval forms. The case study of a copperplate engraving of the Bibliotheca Wolfenbüttel 1705/23 (with A. Ilchmann - published in Nexus Network Journal. Architecture and Mathematics, 25: 685–712.).
Gli ovali di Borromini nella cupola di San Carlo alle Quattro Fontane a Roma (with M. Caputo - to be published in Atti "Francesco Borromini 1599-1667").
ALL SIDES TO AN OVAL
Properties, parameters and Borromini's mysterious construction.
OTHER GAMES (designed by Sophie Püschmann)
CONTATTO!
DIE VERRÜCKTE SCHÜLERZEITUNG
IN-KUBUS
VITA
THE SUNSET GAME - SHELTER
My Resume
Education
Titles
-
Università degli studi di Roma "La Sapienza"
1990 – 1994Dottorato di Ricerca (PhD) in OPERATIONS RESEARCH.
-
1992
Winner of a position as Mathematics teacher in high school having passed written and oral examinations.
-
Università degli studi di Roma “La Sapienza”
1984 – 1989Laurea (BAC+1) in MATHEMATICS, with final mark of 110/110 cum laude.
Grants and scholarships
-
State University of New York, USA
1992-1993One year scholarship at the Department of Applied Mathematics and Statistics in Stony Brook as visiting student NY – USA.
-
Rome
1990 – 199110-month grant at the Istituto Nazionale di Alta Matematica (INDAM)
Work Experience as mathematician
Mathematics consulting for freelance professionals
Teaching of Mathematics (2022-today) at the high school "PHORMS Campus - Berlin Süd" in Berlin
Teaching of Mathematics and basic Computer Science skills (1999-2020) and coordination of the project "Polisportiva Matematici" preparing students to participate in mathematics competitions (since 2009) at the school ITIS "Lattanzio" in Rome
Teaching of Mathematics and basic Computer Science skills at the school IPSIA "T.Minniti" in Guidonia (1993 - 1999)
Private lessons in Mathematics for university and high school students
Written and published material
-
A method for recognising oval forms. The case study of a copperplate engraving of the Bibliotheca Wolfenbüttel 1705/23 (with A. Ilchmann)
2023Published in Nexus Network J. 25: 685–712.
-
Gli ovali di Borromini nella cupola di San Carlo alle Quattro Fontane a Roma (with M. Caputo)
2022Accepted by Atti "Francesco Borromini 1599-1667".
25: 685–712. -
All Sides to an Oval. Properties, Parameters and Borromini's Mysterious Construction. 2nd edition
2019Published by Springer.
-
L'emancipazione dell'ovale.
Aug 1st 2017Published on Galileo – Online scientific journal.
-
All Sides to an Oval. Properties, Parameters and Borromini's Mysterious Construction.
2017Published by Springer.
-
A Euclidean approach to eggs and polycentric curves.
2014Published in Nexus Network J. 16: 345-387.
-
What Borromini might have known about ovals. Ruler and compass constructions.
2014Published in Nexus Network J. 16: 389-415.
-
Asymptotic eigenvalue degeneracy for a class of three-dimensional Fokker-Planck operators.
1995With A.Carlini, M.C.Recchioni e F.Zirilli - on J.Math.Phys. 36.
-
Processi di diffusione riflessi e ottimizzazione globale in un dominio.
1994PhD Thesis.
-
L’uso dei metodi per la ottimizzazione nonlineare nel problema della programmazione lineare.
1989BA Thesis.
Games and puzzles
- Creation of the board game 3 & 4: THE GAME (designed by Sophie Püschmann).
- Creation of the board game DIE VERRUECKTE SCHÜLERZEITUNG (designed by Sophie Püschmann).
- Creation of the board game VITA (designed by Sophie Püschmann).
- Creation of the board game IN-KUBUS (designed by Sophie Püschmann).
- Creation of the board game CONTATTO! (designed by Sophie Püschmann).
- Invention of a Game Application called Polycentrics (patented) for smartphones and tablets (in progress).
- Creation of the table game Il Filmimo on films (patented), together with Luciano Benvenuto (for the prototype) and Annalisa De Rose (for the marketing).
- Creation of crossword puzzles and other puzzles for private use.
- Invention of a way of playing the card game Buraco as a tournament for 5 or 6 players.
- Organisation of tournaments.
- Invention of a Rome-based board for the game Risk! (prototype by Andrea Lupi).
- Contribution to the marketing of the table game Il Grande Gioco del Golf by Luciano Benvenuto, together with Luisa d'Agostino and Annalisa De Rose.
- Coordination for the Di Vittorio–Lattanzio school of the student mathematics games Olimpiadi della Matematica and Kangourou della Matematica.
Personal Competences
Languages
- Italian (mother tongue)
- English (excellent) – C2 certificate
- German (very good) – C1 certificate
- French (good) – eight-year course in public school
Artistic (see also www.angelomazzotti.eu)
- Jazz singing since 2005 (Scuola Popolare di Musica di Testaccio). Classes, workshops, concerts in Italy and in Germany (Berlin)
- Writing of songs or just lyrics in Italian, English and German (since 2008).
- Choir singing since 1983 (CIMA, AMPEM, Todavìa Canta, Sacri Montis, TJazzVoices, Fleeting Glance and ANKA Vocal Band choirs)
- Pop and rock singing since 1985 (concerts in Rome with Penta and Tonic band)
- Folk guitar and singing since 1983 (self-taught). Concerts in Rome and in Germany
- Basic level of piano (SPMT), harmonica, electric bass, percussions.
- Dancing, coreographing and teaching of Tango Argentino from 1996 (studied mainly at the Centro del Tango Argentino “Astor Piazzolla” in Rome). National-TV shows and theatre shows.
- Direction and writing of a theatre musical (Un suono da marciapiede in 1992 at the Teatro de’ Servi in Rome)
- Workshops and/or classes of: acting, modern dancing, circus, swing dance and salsa dance
Computer
- Good level: Geogebra, spreadsheets, word processing, music writing software, search motors
- Basic level: image and audio processing
- Basic level programming: Basic, Fortran, Simscript, Pascal, C++
Organisation and social competences
- Accustomed to working in groups and to collaborating
- Organising groups and communicating
Ovals and Polycentric Curves
My formulas and procedures to draw ovals, eggs and a class of more general polycentric curves can be implemented in CAD software.
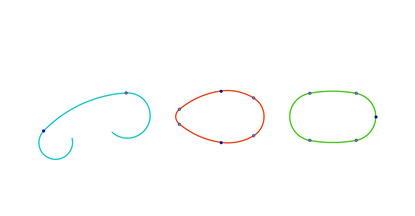
ALL SIDES TO AN OVAL
Properties, parameters and Borromini's mysterious construction. (2nd edition 2019, Springer Ed.)
PAPERS PUBLISHED IN THE NEXUS NETWORK JOURNAL:
A EUCLIDEAN APPROACH TO EGGS AND POLYCENTRIC CURVES
(2014, Nexus Network Journal, 10.1007/s00004-014-0189-5)
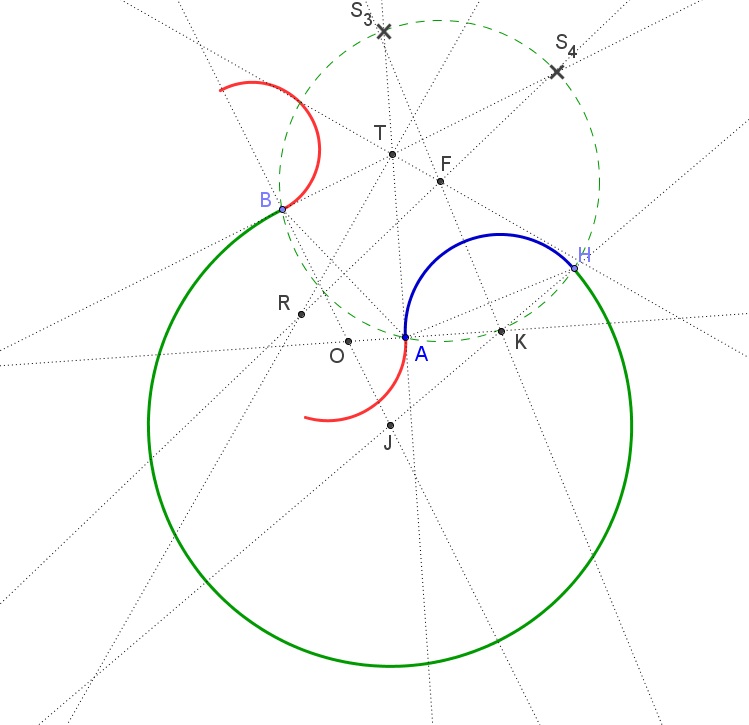
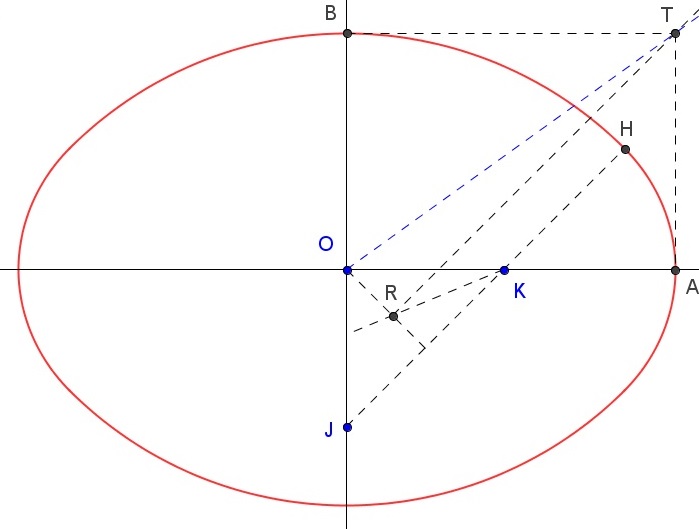
Abstract. I tackle here the problem of smoothly connecting two arcs of curves with two more arcs, and present the application of this procedure to the drawing of a class of egg-shaped curves and to the generation of some open and closed polycentric curves. I provide solid mathematical background as well as ruler and compass constructions, some of them new. The use of basic, although lengthy, Euclidean proof tools suggests these properties and techniques were within reach – if not known – by architects and scientists long before the invention of analytic geometry.
WHAT BORROMINI MIGHT HAVE KNOWN ABOUT OVALS. RULER AND COMPASS CONSTRUCTIONS
(2014, Nexus Network Journal, 10.1007/s00004-014-0190-z)
Abstract. This paper is about drawing ovals once a sufficient number of certain parameters is given. New constructions are displayed, including the case when the symmetry axes are not given. Many of these make use of a recent conjecture by Ragazzo, for which I found a Euclidean proof, thus suggesting it might have been known at the time Borromini chose the ovals for the dome of San Carlo alle Quattro Fontane.
Constructing ovals – Geogebra animation videos
My personal archive of oval constructions.
All constructions are justified by my own mathematical proofs (see the above cited paper).
Ovals of given axis lines, given three independent parameters:
- Oval 01 – given the measure of the axes and the centre of the smaller circumference.
- Oval 02 – given the measure of the axes and the distance of the connecting point from the minor axis.
- Oval 03 - given the measure of the axes and the centre of the bigger circumference.
- Oval 04 - given the measure of the axes and the distance of the junction point from the major axis.
Ovals 01 to 04: Constructing ovals with given axis lines – Ovals 01 02 03 and 04
- Oval 05 - given the measure of the major axis, the centre of the smaller circumference and the distance of the junction point from the minor axis.
- Oval 06 - given the measure of the major axis and the two centres of the circumferences.
- Oval 07 - given the measure of the major axis, the centre of the smaller circumference and the distance of the junction point from the major axis.
- Oval 09 - given the measure of the minor axis and the two centres of the circumferences.
Ovals 05 06 07 and 09: Constructing ovals with given axis lines – Ovals 05 06 07 and 09
- Oval 10 - given the measure of the major axis, the centre of the bigger circle and the distance of the connection point to the major axis.
- Oval 11a - given the measure of the minor axis, the centre of the smaller circle and the distance of the connection point to the minor axis.
Ovals 10 and 11a: Constructing ovals with given axis lines – Ovals 10 and 11a
- Oval 11b - given the measure of the minor axis, the centre of the smaller circle and the distance of the connection point to the minor axis. SECOND CONSTRUCTION.
Ovale 11b: Constructing ovals with given axis lines – Oval 11b
- Oval 12 - given the measure of the minor axis and the two centres of the circumferences.
- Oval 14 - given the measure of the minor axis, the centre of the big circumference and the distance of the junction point from the minor axis.
- Oval 15 - given the minor axis and the distances of the connection point from the two axis.
- Oval 16 - given the minor axis, the centre of the bigger circumference and the distance of the connection point from the major axis.
Ovals 12 14 15 and 16: Constructing ovals with given axis lines – Ovals 12 14 15 and 16
- Oval 17 - given the centres of the two circumferences and the distance of the connection point from the minor axis.
- Oval 18 - given the centre of the smaller circumference and the distances of the connection point from the two axes.
- Oval 19 - given the centres of the two circumferences and the distance of the connection point from the major axis.
- Oval 20 - given the centre of the bigger circumference and the distance of the connection point from the two axes.
Ovals 17 to 20: Constructing ovals with given axis lines – Ovals 17 18 19 and 20
- Oval 21 – given the two axes and the angle of the line of the centres.
- Oval 22 - given the centers of the two circumferences and the ratio between the two axes.
- Oval 23 - given the centre of the small circumference and the radii of both circumferences.
Ovals 21 to 23: Constructing ovals with given axis lines – Ovals 21 22 and 23
Oval with the minimum radius ratio: Oval with minimum ratio of the radii, for any given axis measures
The stadium problem: The stadium problem
Ovals of unknown axis lines, given six independent parameters.
- Oval 106 (U7) of unknown axis lines – given the two vertices on the major axis, the distance of the centre of one of the smaller circumferences to the minor axis and the distance of the connection point to the major axis
- Oval 120 (U21) of unknown axis lines - given two consecutive vertices, the (constrained) connection point and the (constrained) centre of simmetry.
Ovals 106 (U7) and 120 (U21): Ovals with unknown axis lines – Ovals 106 and 120
- Oval 121 (U22) of unknown axis lines – given two consecutive vertices and the centre of the smaller circumference.
- Oval 122 (U23) of unknown axis lines – given two consecutive vertices and the centre of the bigger circumference.
Ovals 121 (U22) and 122 (U23): Ovals with unknown axis lines – Ovals 121 and 122
- Oval 132 (U26) of unknown axis lines - given two centres of consecutive circumferences, their (constrained) connection point and the (constrained) centre of simmetry.
- Oval 160 (U29) of unknown axis lines - given a vertex on the major axis, its centre and a point on the same half oval along with a tangent through it.
Ovals 132 (U26) and 160 (U29): Ovals with unknown axis lines – Ovals 132 and 160
Construction of an egg given four independent centres.
My personal archive of egg constructions.
All constructions are justified by my own mathematical proofs (see the above cited paper).
Construction of an egg given the same centres taken in a different order.
Construction of an egg inscribed inside a trepezium.
Construction of eggs: Constructing a six-centre egg from its centres or inscribing it inside a trapezoid
Constructing certain PCCs – Geogebra animation videos
My personal archive of constructions of polycentric curves.
All constructions are justified by my own mathematical proofs (see the above cited paper).
Four-arc polycentric curves constructed starting from two external arcs.
Given two arcs and a point on each one of them I draw the Connection Locus, made of two circles. Choosing then a point on one or the other circle it is possble to draw two tangent circles. Any choice of four consecutive arcs yields a polycentric curve: Constructing a class of four-arc polycentric curves (PCCSs) by means of the Connection Locus (CL)
Four-arc closed polycentric curves, starting from two connection points and two tangents.
Drawing four-arc closed polycentric curves, starting from two connection points and two tangents, by means of the Connection Locus: Constructing a class of four-arc closed polycentric curves by means of the Connection Locus (CL)
Reviews
- ALL SIDES TO AN OVAL - FREELANCE MATHEMATICS - TEACHING
ALL SIDES TO AN OVAL. Properties, Parameters and Borromini's mysterious Construction
“The book is an original, interesting and opportune contribution to an area not contemplated in geometry courses. “ (U. D'Ambrosio, Mathematical Reviews Clippings, April 2018)
“Angelo Mazzotti’s All Sides to an Oval addresses a fundamental subject for architects, civil engineers and mathematicians involved in designing oval forms or analysing existing ones. The book contains a comprehensive collection of geometrical constructions and mathematical equations on the properties of ovals, the main parameters for managing them, and two case studies of actual built oval forms. In addition, the author poses some new geometrical constructions. A book of this kind on this subject was necessary since only some partial expositions have been previously published. All sections are illustrated with clear drawings that permit an easy understanding. Mazzotti’s training in mathematics and geometry gives him the best skills to carry out this work. [ ] Angelo Mazzotti’s All Sides to an Oval is a fundamental book for anyone working with oval forms from the point of view of the geometric control of the shapes.” (Ana López-Mozo, book review in Nexus Netw J (2018) 20:303–304)
“Everything is clearly explained and the many illustrations produced with geogebra are crystal clear. It might however be interesting to have a look at the associated website www.mazzottiangelo.eu/en/pcc.asp where you find links to YouTube videos showing animated geogebra constructions. […] For the mathematician, it is invaluable because it brings together so much information that was either not known or never written down or if it was, then at least it was scattered in diverse publications." (Adhemar Bultheel, European Mathematical Society, euro-math-soc.eu, March 2017)
"This interesting book deals with surprising properties of polycentric ovals and applications. [...] The text and the figures are very readable. The historical remarks and the fields of applications are interesting. The book is enjoyable not only for mathematicians." (Agota H. Temesvari, zbMATH, 2017)
"Angelo Alessandro Mazzotti, professeur à ITC Di Vittorio à Rome, leur a consacré cette étude exhaustive, avec de très nombreuses figures et illustrationsè[...] Nous avons particulièrement apprécié le catalogue des ovales à quatre centres les plus remarquables, utilisés dans l’architecture aux XVIème et XVIIème siècles. Ce livre intéressera également les amateurs d’architecture classique car il comporte des descriptions très complètes des ovales de Borromée du dome de l’église Saint-Charles-aux-quatre-fontaines à Rome, ou encore des ovales figurant dans le plan du Colysée.” (from the book Fous de codes (Secrets) by Mark Frary, Flammerion Ed., 2018)
FREELANCE MATHEMATICS
„Ho avuto più occasioni di beneficiare delle consulenze matematiche del Dr. Mazzotti. I suoi contributi matematici in materia finanziaria, di lavori pubblici e analisi della produzione si sono sempre rivelati precisi e perfettamente rispondenti alle mie esigenze."
(Architetto Roberto Pignocchi, Roma 2023)
TEACHING
„[…] Ihre Nachhilfe trägt rasch Früchte und ich wollte mich direkt bedanken für Ihre Hilfe. Es lohnt sich!“
(Email from parent of a private lesson student – Berlin 2022)
"[…] credo che lei già sappia che lei rimarrà sempre nel cuore di tutti coloro che l'hanno conosciuta come uno degli elementi più preziosi che il nostro istituto abbia mai avuto...ho sempre potuto contare su di lei, sulle sue osservazioni, sul suo contributo sincero e costruttivo, sulle tante iniziative che ha reso possibile realizzare”
(Email from the Headmaster of the high school “Di Vittorio-Lattanzio” – Rome 2020)
„[…] Ma non mi lascio sfuggire l'occasione di salutarla e di augurarle il meglio perché se lo merita davvero, perché anche se sono una frana in matematica se non fosse per lei sarei rimasto ancora alle equazioni di primo grado. Insomma grazie di tutto prof, grazie perché in un certo senso sono cresciuto con lei, entrando a 14 anni e la saluto ora che ne ho 20. Mi dispiace non fare l'esame di maturità con lei ma spero di poter prendere un caffé a quella macchinetta un giorno con il mio professore preferito.” (Email from a high school student– Rome 2020)
Contact
- Phone (it): 0039 339 4940 558
- Phone (de): 0049 3039 746536
- Email : angelomazzotti@gmail.com